Abstract
In Wada et al. (2019), we proposed for the first time that a new class of planets, blanets, can be formed around supermassive black holes in the galactic center. Here, we investigate the dust coagulation processes and physical conditions of the blanet formation outside the snowline (rsnow ∼ several parsecs) in more detail, especially considering the effect of the radial drift of the dust aggregates. We found that a dimensionless parameter 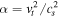 , where vt is the turbulent velocity and cs is the sound velocity, describing the turbulent viscosity should be smaller than 0.04 in the circumnuclear disk to prevent the destruction of the aggregates due to collision. The formation timescale of blanets τGI at rsnow is, τGI ≃ 70–80 Myr for α = 0.01 − 0.04 and MBH = 106M⊙. The mass of the blanets ranges from ∼20ME to 3000ME in r < 4 pc for α = 0.02 (ME is the Earth mass), which is in contrast with 4ME–6ME for the case without the radial drift. Our results suggest that blanets could be formed around relatively low-luminosity active galactic nuclei (Lbol ∼ 1042 erg s−1) during their lifetime (≲108 yr).
, where vt is the turbulent velocity and cs is the sound velocity, describing the turbulent viscosity should be smaller than 0.04 in the circumnuclear disk to prevent the destruction of the aggregates due to collision. The formation timescale of blanets τGI at rsnow is, τGI ≃ 70–80 Myr for α = 0.01 − 0.04 and MBH = 106M⊙. The mass of the blanets ranges from ∼20ME to 3000ME in r < 4 pc for α = 0.02 (ME is the Earth mass), which is in contrast with 4ME–6ME for the case without the radial drift. Our results suggest that blanets could be formed around relatively low-luminosity active galactic nuclei (Lbol ∼ 1042 erg s−1) during their lifetime (≲108 yr).
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
There is enough evidence suggesting that planets are formed in the circumstellar disks around stars. However, stars might not be the only site for planet formation. Recently, in Wada et al. (2019, hereafter Paper I), we claimed a new class of "planets" 5 that orbit around supermassive black holes (SMBHs) in galactic centers. Paper I theoretically investigated the growth processes of planets, from sub-micron-sized icy dust monomers to Earth-sized bodies outside the snowline in a circumnuclear disk around an SMBH, typically located several parsecs from the SMBHs. As is the case in a protostellar disk, in the early phase of the dust evolution, low-velocity collisions between dust particles promote sticking; therefore, the internal density of the dust aggregates decreases with growth (Okuzumi et al. 2012; Kataoka et al. 2013). When the size of porous dust aggregates reaches 0.1–1 cm, the collisional and the gas-drag compression become effective, and as a result, the internal density stops decreasing. Once 10–100 m sized aggregates are formed, they decouple from gas turbulence, and as a result, the aggregate layer becomes gravitationally unstable (Michikoshi & Kokubo 2016, 2017), leading to the formation of "planets" due to the fragmentation of the layer, with ten times the mass of the earth. The objects orbit the SMBHs with an orbital time of 105–106 yr. To distinguish them from standard planets, we hereafter call these hypothetical astronomical objects blanets. 6
The results reported in Paper I, however, have two major limitations. One is that the collisional velocity between the dust aggregates might become too large (>several 100 m s−1 at the Stokes parameter, St
∼ 1). And if the collisional velocity is that large, rather than growing, the aggregates might get destroyed. In Paper I, we used the numerical experiments conducted by Wada et al. (2009).
7
on the collisions between the dust aggregates, wherein the critical collisional velocity (vcrit) scales with the mass md
of the dust aggregates, as  . However, this is correct only for the head-on collisions, as stated in the paper. Moreover, Wada et al. (2009, 2013) showed that the growth efficiency of the dust aggregates depends on the impact parameter of the collisions, and as a result, vcrit does not strongly depend on the mass of the dust aggregates, if offset collisions are taken into account. They concluded that vcrit ≃ 80 m s−1 for the ice monomers.
8
This low critical velocity is also one of the obstacles in the planet formation in circumstellar disks. In this follow-up paper, we adopt vcrit ≃ 80 m s−1 as a constraint on the growth of the dust aggregates.
. However, this is correct only for the head-on collisions, as stated in the paper. Moreover, Wada et al. (2009, 2013) showed that the growth efficiency of the dust aggregates depends on the impact parameter of the collisions, and as a result, vcrit does not strongly depend on the mass of the dust aggregates, if offset collisions are taken into account. They concluded that vcrit ≃ 80 m s−1 for the ice monomers.
8
This low critical velocity is also one of the obstacles in the planet formation in circumstellar disks. In this follow-up paper, we adopt vcrit ≃ 80 m s−1 as a constraint on the growth of the dust aggregates.
Another limitation of Paper I is that the size of dust aggregates ad and collisional velocity Δv show runaway growth in the collisional compression phase around St ∼ 1. However, this rapid growth would not be realistic if a more natural treatment of the internal density of the dust is considered (Section 2.2.1, see also Section 3).
Moreover, there is a critical process that may promote blanet formation. In paper I, we did not take into account the radial drift of the dust particles as the first approximation. The radial velocity of the dust vr,d
relative to the gas (Weidenschilling 1977; Tsukamoto et al. 2017) is vr,d
∼ St
η
vK
, and  , where cs
is the gas isothermal sound velocity and vK
is the Keplerian rotational velocity. In the circumnuclear disk around an SMBH, initially St
η ∼10−4–10−3. Then the drift time of the dust particle tdrift ∼ r/vr,d
∼ 5–50
, where cs
is the gas isothermal sound velocity and vK
is the Keplerian rotational velocity. In the circumnuclear disk around an SMBH, initially St
η ∼10−4–10−3. Then the drift time of the dust particle tdrift ∼ r/vr,d
∼ 5–50  Myr. This is not negligibly small for the lifetime of the active galactic nucleus (AGN), i.e., 107 − 108 yr. In this paper, we investigate the effects of the radial drift of the dust particles.
Myr. This is not negligibly small for the lifetime of the active galactic nucleus (AGN), i.e., 107 − 108 yr. In this paper, we investigate the effects of the radial drift of the dust particles.
The remainder of this paper is organized as follows. In Section 2, we describe the models for the dust evolution and its application to the circumnuclear region. In Section 3, we show the results of the models with and without the radial drift of the dust particles. In Section 4, we discuss how the maximum collisional velocity and the formation timescale of blanets depend on the parameters α and MBH. We also discuss the expected mass of the blanets and their radial distribution. Finally, we summarize the results in Section 5.
2. Models
2.1. The Region of "Blanet Formation"
Here we briefly summarize the concept of dust evolution around SMBHs, as discussed in Paper I. Figure 1 shows a schematic of the AGN and the circumnuclear disk. An SMBH (with a mass of 106–1010 M⊙) is surrounded by an accretion disk, which radiates enormous energy (the bolometric luminosity is ∼1042–1045 erg s−1), mostly as ultraviolet and X-rays. The dust particles in the central r < rsub are sublimated by the radiation from the accretion disk around the SMBH. The radius depends on the AGN luminosity:

where LUV is the ultraviolet luminosity of the AGN, and ad is the dust size (Barvainis 1987). The radiation forms conical ionized gas (narrow emission-line region) and also contributes to producing the outflows of the dusty gas and torus (Wada 2012; Izumi et al. 2018; Wada et al. 2018). In the mid-plane of the torus, cold, dense gas forms a thin disk, where icy dust particles can be present beyond the snowline rsnow (see Section 2.4).
Figure 1. A schematic picture of the AGN and the circumnuclear disk.
Download figure:
Standard image High-resolution imageWe introduce a free parameter  , where cs
is the gas sound velocity and vt
is the turbulent velocity, to represent strength of the kinematic viscosity due to the turbulence (e.g., Ormel & Cuzzi 2007, see also Equations (7) and (8)). In the circumnuclear disk in AGNs, the value of α is highly uncertain.
9
Therefore, we here treat α as a free parameter to check how it alters the results, especially the maximum collisional velocity between the dust aggregates and the onset of the gravitational instability of the dust disk.
, where cs
is the gas sound velocity and vt
is the turbulent velocity, to represent strength of the kinematic viscosity due to the turbulence (e.g., Ormel & Cuzzi 2007, see also Equations (7) and (8)). In the circumnuclear disk in AGNs, the value of α is highly uncertain.
9
Therefore, we here treat α as a free parameter to check how it alters the results, especially the maximum collisional velocity between the dust aggregates and the onset of the gravitational instability of the dust disk.
In contrast to the dust coagulation process in the circumstellar disks (Weidenschilling 1977), the drag between dust particles and gas obeys the Epstein law. The aggregate's size (ad
) is always much smaller than the mean free path of the gas,  , where σmol and nmol are the collisional cross-section and number density of the gas, respectively.
, where σmol and nmol are the collisional cross-section and number density of the gas, respectively.
2.2. Evolution of Dust Aggregates in Each Stage
The model for the growth of dust particles here is based on the elementary processes found around stars. The evolution of dust particles is divided into four stages as described below.
2.2.1. Hit-and-stick Stage
If the dust aggregates grow through ballistic cluster-cluster aggregation (BCCA), the internal structure of the aggregate should be porous (i.e., the internal density is much smaller than the monomer's density: ρint ≪ ρ0), and its fractal dimension is D ≃ 1.9 (Mukai et al. 1992; Okuzumi et al. 2009). This is called the hit-and-stick stage (Okuzumi et al. 2012; Kataoka et al. 2013), and the internal density is given by

where md is the mass of the aggregate, and m0 is the monomer's mass. We assume that m0 = 10−15 g and ρ0 = 1 g cm−3.
The growth rate for md is

where Σd is the surface density of the dust disk, Δv is collision velocity between the aggregates, and Hd is the scale height of the dust disk as given in (Youdin & Lithwick 2007; Tsukamoto et al. 2017)

where Hg
= cs
/ΩK
is the scale height of the gas disk, and St
is the Stoke parameter, i.e., the normalized stopping time is defined as St
≡ tstop/tL
with the eddy turn over time tL
. Here we suppose that  and
and

where Σg is the gas surface density.
The collision velocity between aggregates Δv for St
< 1 can be divided into two regimes (Ormel & Cuzzi 2007): regime I)  , and regime II)
, and regime II)  . Here the Reynolds number,
. Here the Reynolds number,  with the molecular viscosity
with the molecular viscosity  is
is

For the hit-and-stick stage,  , then for the regime I,
, then for the regime I,

where St,1 and St,2 are Stokes numbers of the two colliding particles, and CI is a constant of the order of unity (Sato et al. 2016). For regime II, on the other hand,

where vL is velocity of the largest eddy. We assume that ΔvI = ΔvII at the transition.
The size of dust aggregates determines how they interact with the gas. The dynamics of the aggregates is affected by their cross sections, which depend on their internal inhomogeneous structure. The radius of BCCA cluster aBCCA consisted of N monomers (N = md /m0) is given as aBCCA ≃ N0.5 a0 for N ≫ 1 (Mukai et al. 1992; Wada et al. 2008, 2009), which was also confirmed through N-body simulations (Suyama et al. 2012). We then assume that

2.2.2. Compression Stages
The hit-and-stick stage ends due to collisions between the aggregates (collisional compression), or due to their interaction with the ambient gas (gas-drag compression). In the collisional compression, the rolling energy Eroll, which is the energy required to rotate a particle around a connecting point by 90°, is comparable to the impact energy, Eimp = md Δv2/4, between the two porous dust aggregates of the same mass, md . Beyond this point, the aggregates start to get compressed due to mutual collisions and interaction with the gas (i.e., the ram pressure).
According to Suyama et al. (2012), the internal density of the aggregated ρint,f formed by collisions between two equal-mass aggregates, with density ρint, is calculated for Eimp > 0.45 Eroll:

ρf
is the fractal density of the dust aggregate:  , and Eroll = 4.37 × 10−9 erg.
, and Eroll = 4.37 × 10−9 erg.
Moreover, the fluffy dust aggregates can be compressed owing to the ram pressure of the ambient gas (Kataoka et al. 2013). The internal density of the aggregates that are compressed by the gas is given

where the ram pressure for a dust aggregate is

with the stopping time ts = St /ΩK (Kataoka et al. 2013).
As the aggregates become more massive (md
> 1010 g), they start getting compressed owing to their self-gravity, and the internal density evolves as  (Okuzumi et al. 2012).
(Okuzumi et al. 2012).
2.2.3. N-body Stage
When St ≃ 1, kinematics of the aggregates is affected not only by the turbulence, but also by mutual interaction between the aggregates as an N-body system and by the gravitational interaction with the density fluctuation due to the turbulence. Then the collision velocity between the aggregates is determined by a balance between various heating and cooling processes as the N-body particles. According to Michikoshi & Kokubo (2016, 2017), we solve the following equation to get the equilibrium random velocity of the dust aggregates vd ,

The first three heating terms represent the gravitational scattering of the aggregates, stirring by the turbulence, and gravitational scattering by density fluctuation of the turbulence, respectively. The two cooling terms in Equation (13) represent the collisional damping and the gas drag. We assume the collision velocity Δv ≈ vd at St = 1 and numerically solve Equation (13) in this stage.
2.2.4. Radial Drift of the Dust Particles
In Paper I, we ignored the radial drift of the dust particles in the disk. However, as mentioned in Section 1, this is not always obvious. Here, we solve the following governing equations for the dust evolution based on the assumption that the mass distribution of the dust particles at each orbit radius is singly peaked at a mass (Sato et al. 2016; Tsukamoto et al. 2017);


Here tcoll in Equation (15) is the collision time, and the source term is

where nd is the number density of the dust particles.
The dust particles have a radial velocity due to the drag with the ambient gas:

where vK is the Kepler velocity and η is a parameter that determines the sub-Keplerian motion of the gas, and the radial velocity of the gas vr,g
is given with the mass accretion rate  :
:

where the mass accretion rate  is assumed to be using the Eddington mass accretion rate
is assumed to be using the Eddington mass accretion rate  with the Eddington ratio γEdd.
with the Eddington ratio γEdd.
2.3. Gravitational Instability of the Dust Disk and Formation of Blanets
We investigate the gravitational instability (GI) of the disk consisting of dust aggregates with St > 1 using the Toomre's Q-value defined as

For the axisymmetric mode, Qd < 1 is the necessary condition for GI, but the non-axisymmetric mode can develop for Qd ≲ 2. In this case, spiral-like density enhancements are formed followed by fragmentation of the spirals (Michikoshi & Kokubo 2017), which leads formation of massive objects, i.e., blanets. The mass of blanets is estimated as

where the critical wavelength for GI is

2.4. Initial and Boundary Conditions
In all the models, the circumnuclear cold gas disk embedded in the geometrically thick torus (see Figure 1) is assumed to be gravitationally stable; the Toomre's Q-value, Qg
≡ cs
ΩK
/π
GΣg
= 2. The gas sound velocity is assumed to be  with Tg
= 100 K and μ = 2.0.
with Tg
= 100 K and μ = 2.0.
The Eddington ratio is assumed to be γEdd = 0.01. The AGN bolometric luminosity is then Lbol = 1.3 × 1042erg s−1 MBH/(106 M⊙). The X-ray luminosity of the AGN, which is used to determine the snowline radius, LX = 0.1Lbol. This can be attributed to the fact that the UV flux from the accretion disk is attenuated in the dense circumnuclear disk.
The snowline for ad = 0.1 μm,

Therefore, it is expected that the dust in the most part of the circumnuclear disk is icy. We assume Tice = 170 K. The dust-to-gas mass ratio is assumed as fdg = 0.01. We solve the governing equations (Section 2.2.4) between r = 0.1 pc and 200 pc with 600 grid cells.
3. Results
Figure 2(a) shows a typical evolution of a dust aggregate at the snowline for MBH = 106 M⊙ and α = 0.02. The internal density of the aggregate ρint is plotted as a function of its mass md . Initially, the internal density decreases monotonically from the monomer's initial density, i.e., ρ0 = 1 g cm−3 to 4 × 10−6 g cm−3, as its mass increases from md ∼ 10−15 g to ∼10−5 g. At that instant, the size of the aggregate becomes ∼1 cm (see Figure 2(b)). After this hit-and-stick phase, the fluffy dust aggregates keep growing due to collisions in the turbulent gas motion until St ≃ 1. During this stage (md = 10−5 g to 1010 g), the aggregates are compressed mainly due to the gas drag (Section 2.2.2), and therefore ρint gradually increases. 10 After St ≳ 1, the aggregates behave as an N-body system under the effect of the turbulent fluctuation (Equation (13)). For md > 1010 g and St > 1, the aggregates are compressed due to their self-gravity. In the model shown in Figure 2, it becomes gravitationally unstable at t = 75 Myr (see also Section 4.1).
Figure 2. (a) Evolution of the internal density of a dust aggregate ρint at the snowline (r = 1.5 pc) as a function of the aggregate mass md for MBH = 106 M⊙ and α = 0.02. Evolution prior to the gravitational instability (i.e., Qd > 2) is plotted. The positions where St becomes unity and Qd = 2 are shown by the filled white and black circles, respectively. The color bar represents the Stokes number. (b) Same as (a), but for collision velocity of the aggregates Δv and size of the aggregate ad . The dashed line shows Δv = 80 m s−1, which is the limit for the collisional destruction of the aggregates suggested by numerical experiments (Wada et al. 2009). After St = 1 is attained, Δv drops and the disk of the aggregates becomes gravitationally unstable.
Download figure:
Standard image High-resolution imageFigure 2(b) plots the collisional velocity Δv of the aggregate and its size ad as a function of md . The size ad monotonically increases. In the compression stage (md > 105 g), the increase of ad slows down (see Equation (9)). Initially Δv is 20 cm s−1, and it slightly decreases during the hit-and-stick stage. Then it turns to an increase phase until ∼57 m s−1 around St = 1 during the compression stage. The size of the aggregate becomes ad ∼ 104 cm at the end of this stage. In this case, the aggregates are not compressed by their self-gravity (md < 1010 g) before the dust disk becomes GI. Note that the increase of Δv slows down at md ∼ 0.1 g, which corresponds to the transition between ΔvI and ΔvII (Equations (7) and (8)).
The growth time of an aggregate for  can be estimated as
can be estimated as

Figure 3 shows time evolution of ρint, ad , St , and Δv for the same model shown in Figure 2. The hit-and-stick phase lasts for ∼10 Myr as expected by tgrow, and St becomes unity at t = 60 Myr. At this moment, the dust aggregate's size reaches ∼100 m (Figure 3(b)).
Figure 3. Time evolution of the internal density of the aggregate ρint, surface density of dust Σd , size ad and collision velocity Δv for the same model shown in Figure 2. Evolution prior to the gravitational instability is plotted. The position where St = 1 for each quantity is shown by a white filled circle. The maximum Δv is shown (57.3 m s−1 in this case) and the critical velocity for the collisional destruction (i.e., 80 m s−1) is shown by the red-dotted line in panel (c).
Download figure:
Standard image High-resolution imageFigure 3(b) shows that the growth of ad is exponential, or slower in time, in contrast to the results in Paper I. This is a natural consequence of the evolution of the mass of the dust aggregates. The mass increase rate of the dust is

Here we assume the dust layer is sedimented, i.e., its thickness Hd
is scaled as  . For
. For  (Equation (8)), dmd
/dt ∝ md
, therefore, md
grows exponentially. The runaway growth seen in Paper I is caused by the assumption that the internal density of the dust aggregates stays porous (i.e., the fractal dimension is ∼2) through the evolution. In reality, when the compression by the ambient gas works, ρint is nearly constant (i.e.,
(Equation (8)), dmd
/dt ∝ md
, therefore, md
grows exponentially. The runaway growth seen in Paper I is caused by the assumption that the internal density of the dust aggregates stays porous (i.e., the fractal dimension is ∼2) through the evolution. In reality, when the compression by the ambient gas works, ρint is nearly constant (i.e.,  ), as shown in Figure 2, therefore St
∝ ad
. If the scale height of the dust disk is constant, then
), as shown in Figure 2, therefore St
∝ ad
. If the scale height of the dust disk is constant, then  therefore, the growth of the dust aggregate should be slower than
therefore, the growth of the dust aggregate should be slower than  .
.
Figure 3(c) shows that the collisional velocity Δv gradually decreases during the hit-and-stick stage, and it turns to rapid increase during the compression stage until St becomes unity at t = 56 Myr. In the N-body stage, the collisional velocity decreases from its maximum value, 57 m s−1, and it becomes GI (i.e., Qd ≤ 2) at t ≃ 75 Myr.
For comparison, the evolution of the model without the radial drift is shown in Figure 4. We found that the dust aggregates before St = 1 evolve almost the same way as that in the model with the radial drift (Figure 3). However, the time for GI is 136 Myr, in contrast to 71 Myr for the case with the advection.
Figure 4. Same as Figure 3, but the model without the radial drift of the dust. Note that the time of GI is 136 Myr, in contrast to 71 Myr in Figure 3.
Download figure:
Standard image High-resolution imageFigure 5 shows the radial distributions of Σd , Hd , Δv, the radial velocity of the dust and gas (vr,d and vr,g ), ρint, St , md , and ad at 200 Myr in the same model shown in Figure 2. As Figure 5(a) shows, the dust is accumulated around r ∼ 2 − 3 pc, where vr,d ≪ vr,g (Figure 5(c)) and St turns from St < 1 to St > 1 (Figure 5(b)). From Figure 5(d), the dust aggregates evolve more rapidly in the inner region (r ≲ 3 pc), and the maximum size is ∼km. We call these objects as blanetesimals.
Figure 5. Radial distribution of various quantities at t = 200 Myr for the same model shown in Figure 2. (a) Surface density of dust Σd and the scale height of the dust Hd . The gray line is Σd at t = 0. Note that the surface density of the dust decreases in the outer disk (r > 30 pc), and the total mass of the dust is conserved. The vertical dashed line is the position of the snowline rsnow = 1.5 pc. (b) Same as (a), but for the collision velocity Δv, the internal density of the aggregate ρint and the Stokes parameter St . (c) Same as (a), but for the radial velocity of the dust vr,d and vr,g normalized by the Kepler velocity vK. (d). Same as (a), but for the mass and size of the aggregate, md and ad .
Download figure:
Standard image High-resolution image4. Discussion
4.1. Dependence on α and MBH.
In the models with the radial drift of the dust aggregates, we investigated how the maximum velocity of the collision  and the time for GI (τGI) depend on α and MBH. In Figure 6, we plot
and the time for GI (τGI) depend on α and MBH. In Figure 6, we plot  and τGI as a function of α for MBH = 106
M⊙ and 107
M⊙. It shows that
and τGI as a function of α for MBH = 106
M⊙ and 107
M⊙. It shows that  depends on α, and not on MBH. If
depends on α, and not on MBH. If  m s−1 is necessary for collisional growth as numerical experiments suggested (Wada et al. 2009), then α should be ∼0.04 or smaller.
m s−1 is necessary for collisional growth as numerical experiments suggested (Wada et al. 2009), then α should be ∼0.04 or smaller.
Figure 6. (a)  as a function of α in the models with the radial drift. Red and green crosses are MBH = 106
M⊙ and 107
M⊙, respectively. The dotted line is the velocity limit for collisional destruction (80 m s−1). (b) Time for the gravitational instability (GI) as a function of α. The filled circles are the time for GI and the open circles are the time for St
= 1. Red and green circles are MBH = 106
M⊙ and 107
M⊙, respectively. The α corresponds to
as a function of α in the models with the radial drift. Red and green crosses are MBH = 106
M⊙ and 107
M⊙, respectively. The dotted line is the velocity limit for collisional destruction (80 m s−1). (b) Time for the gravitational instability (GI) as a function of α. The filled circles are the time for GI and the open circles are the time for St
= 1. Red and green circles are MBH = 106
M⊙ and 107
M⊙, respectively. The α corresponds to  m s−1, i.e., α = 0.04 is shown by the blue dotted line.
m s−1, i.e., α = 0.04 is shown by the blue dotted line.
Download figure:
Standard image High-resolution imageThe behavior of the dust growth (e.g., Figure 2) does not significantly depend on α and MBH, but the timescale to reach St = 1 is different as shown in Figure 6(b). For example, for MBH = 106 M⊙ and α = 0.02, it takes ∼60 Myr when St exceeds unity, whereas it is ∼225 Myr for MBH = 107 M⊙ and α = 0.02. This implies that smaller BHs may preferentially host blanets within a lifetime AGNs (≲108 yr). Figure 6(b) shows that, for MBH = 107 M⊙, the blanetesimal disk may not become GI earlier than ∼150 yr for α < 0.04. For α > 0.05 or 0.06, GI does not occur at r = rsnow in the models with MBH = 106 M⊙ or 107 M⊙, respectively.
4.2. Number and Mass of Blanets
In the final stage of the evolution, the blanetesimal disk can be gravitationally unstable, and it fragments into massive objects, i.e., blanets (see Section 2.3). Figure 7 shows the radial distribution of the mass and typical separation between blanets, λbl ≈ λGI (Equation (21)). Two models with the radial drift for MBH = 106 M⊙ with α = 0.02 and MBH = 107 M⊙ with α = 0.04 are shown. For comparison, a model without the radial drift is also shown (MBH = 106 M⊙ and α = 0.02). The mass of blanets ranges from ≃ 20ME at r = rsnow to ≃3000ME at r ∼ 3.5 pc for MBH = 106 M⊙, in contrast to the model without advection, which is Mbl ≃ 3ME − 7ME . For MBH = 107 M⊙, Mbl ≳ 104 ME − 105 ME outside the snowline. However, this extraordinary massive blanet is unlikely, because it is comparable to the minimum mass of brown dwarfs (∼2 × 104 ME ). Therefore, the largest size of the blanets (Rbl) would be maximally ∼10 × Earth's radius at r ∼ 3 pc for MBH = 106 M⊙, if the average internal density is similar to that of the Earth.
Figure 7. Radial distribution of mass in the Earth mass ME (solid lines) for the left vertical axis, and the critical wavelength for GI (λbl) by the dashed lines for the right vertical axis. The advection models for MBH = 106 M⊙, α = 0.02 (blue) and MBH = 107 M⊙, α = 0.04 (green) are shown in blue and green lines, respectively. The model without advection (α = 0.02) is shown by orange lines. The blue and green vertical dotted lines are position of snowlines for MBH = 106 M⊙ and MBH = 107 M⊙, respectively.
Download figure:
Standard image High-resolution imageNumber of blanets is ∼ 8 ×105 at r = rsnow for MBH = 106 M⊙ with α = 0.02, provided that all the dust is converted to blanets through GI. From Figure 7, the average distance between blanets would be λbl ∼ 10−3 pc at r = rsnow. Therefore, the system of blanets does not resemble any known exoplanet systems, in a sense that the "planets" are isolated, dominant objects in their orbits.
Is the swarm of blanets the final form of the system? The collisional timescale tcoll for the blanets can be estimated as

where where nbl and σbl are the number density and velocity dispersion of the blanets, respectively. rcoll is the distance at the closest approach, which is rcoll ∼ 2Rbl (Binney & Tremaine 2008). The second term of Equation (25) represents the gravitational focusing, which enhances the collision rate. For  , Mbl ≃ 20ME
, Rbl ≃ 3RE
, and σbl ∼ Δv ≃ 30 m s−1 (Figure 3(c)), the collisional time is tcoll ≈ 6 Gyr. This can be shorter, if three-body encounters between a close-binary and a blanet are considered. Therefore, the blanet system could dynamically evolve in the cosmological timescale, and it would be interesting study the evolution by direct N-body simulations.
, Mbl ≃ 20ME
, Rbl ≃ 3RE
, and σbl ∼ Δv ≃ 30 m s−1 (Figure 3(c)), the collisional time is tcoll ≈ 6 Gyr. This can be shorter, if three-body encounters between a close-binary and a blanet are considered. Therefore, the blanet system could dynamically evolve in the cosmological timescale, and it would be interesting study the evolution by direct N-body simulations.
4.3. Can Blanets Acquire a Massive Gas Envelope?
It would be interesting to investigate whether blanets can obtain an atmosphere. If the Hill radius rH
of a blanet is larger than the disk scale height, the blanets may form a gap, then the obtained mass of the atmosphere depends on rH
. The Hill radius of a blanet,  is
is

whereas the scale height of the gas disk at r = 1.5 pc for MBH = 106
M⊙ is,  pc, which is larger than rH
.
pc, which is larger than rH
.
On the other hand, the Bondi radius is

Therefore, we suspect that the mass of the atmosphere is limited by the Bondi accretion, rather than by a gap formation. If this is the case, the envelope mass would be


However, if the Bondi radius is filled with the ambient gas during the orbital motion of a blanet, the envelope mass could be maximally

for Mbl = 1000ME at rbl = 1.5 pc. The small Menv would suggest that the runway accretion of the gas to blanets and formation of massive "gas giants" are difficult, but it also depends on how quickly are the orbits of blanets filled with the gas. This is an interesting open question for future studies.
4.4. Can Other Mechanisms of Planet Formation Be Applicable?
In this paper, we focused on the evolution of the dust aggregates based on the coagulation theories of dust monomers and the gravitational instability. Other formation mechanisms of planetesimals have also been proposed and extensively discussed in the planet formation community. Among them, we here look over the pebble accretion, secular gravitational instability (secular GI), and the streaming instability as possible mechanisms of blanetesimal formation. More quantitative analysis in the circumnuclear environment would be interesting for future studies.
The pebble accretion is an accretion process of small solid bodies (i.e., pebbles) to massive seed objects (e.g., planets or planetesimals) under the effect of the gas drag and gravity (e.g., Ormel 2017; Lambrechts et al. 2019). In the present case, relatively massive aggregates could accumulate ambient smaller particles, then they could become more massive. However, the timescale conditions for the pebble accretion (Ormel & Liu 2018), i.e., tsettl < tenc and tstop < tenc are not likely to be satisfied in the circumnuclear disk, where the settling time tsettl is the time needed for a particle to sediment to the massive objects, and the encounter time tenc is the duration of the gravitational encounter time. In other words, the radial flux of pebbles due to the gas drag is too small in the region of St ≪ 1. Moreover, the relatively large turbulent motion of the gas (i.e., α ≳ 0.01) may prevent from the pebble accretion (Ormel & Liu 2018), in contrast to the circumstellar disk. Therefore, we do not expect that the pebble accretion is a major process as a formation mechanism of blanets.
The secular GI, which is the gravitational instability due to gas-dust friction, is another possible mechanism to form planets in the circumstellar disk (Youdin 2011). According to Takahashi & Inutsuka (2014), the condition for this instability is expressed as

In the present case, Γ ∼ 100 for α ≳ 0.01, fdg = 0.01, η ∼ 10−4 and Qg = 2, therefore, we do not expect the secular GI in the circumnuclear disk.
The streaming instability could be an effective mechanism to make condensations of dust particles, if the dust-to-gas mass ratio (fdg ) is close to unity (e.g., Youdin & Goodman 2005). According to numerical simulations by Carrera et al. (2015), coagulation of particles driven by the streaming instability depends on fdg and St . They found that the streaming instability occurs for fdg ∼ 0.02 for St ∼ 0.1. In our case, the dust-to-gas mass ratio increases to fdg ≃ 0.02 − 0.03 from the initial value (0.01) outside the snowline due to the radial drift of the dust aggregates. However, St ≫ 1 in the region (Figure 5(b)), therefore we do not expect that the streaming instability occurs in the circumnuclear disk.
5. Summary
In this follow-up paper of Wada et al. (2019) (Paper I), we theoretically investigated a process of dust evolution around an SMBH in the galactic center. We proposed that a new class of astronomical objects, blanets can be formed, provided that the standard scenario of planet formation is present in the circumnuclear disk.
Here, we investigated the physical conditions of the blanet formation outside the snowline (rsnow ∼ several parsecs) in more detail, especially considering the effect of the radial drift of the dust aggregates. We also improved the dust evolution model in Paper I in terms of the internal density evolution of the dust aggregates. We assumed the maximum collisional velocity for destruction, which was suggested by previous numerical simulations, as one of the necessary conditions for blanet formation. We found that a dimensionless parameter  , where vt
is the turbulent velocity and cs
is the sound velocity, describing the effective angular momentum transfer due to the turbulent viscosity in the circumnuclear disk should be smaller than 0.04 for the black hole mass MBH = 106
M⊙; otherwise, the dust aggregates could be destroyed due to collisions. The formation timescale of blanets τGI at rsnow is τGI ≃ 70–80 Myr for α = 0.01 − 0.04. The blanets (Mbl) are more massive for larger radii; they range from Mbl ∼ 20ME
− 3000ME
in r < 4 pc, in contrast to Mbl = 3 − 7ME
for the case without the radial drift.
, where vt
is the turbulent velocity and cs
is the sound velocity, describing the effective angular momentum transfer due to the turbulent viscosity in the circumnuclear disk should be smaller than 0.04 for the black hole mass MBH = 106
M⊙; otherwise, the dust aggregates could be destroyed due to collisions. The formation timescale of blanets τGI at rsnow is τGI ≃ 70–80 Myr for α = 0.01 − 0.04. The blanets (Mbl) are more massive for larger radii; they range from Mbl ∼ 20ME
− 3000ME
in r < 4 pc, in contrast to Mbl = 3 − 7ME
for the case without the radial drift.
The typical separations between the blanets, estimated from the wavelength of the gravitational instability, would be ∼10−3–10−2 pc.
For MBH ≥ 107 M⊙, the formation timescale is longer than ∼150 Myr for α ≤ 0.04. Although the GI of the blanetesimal disk takes place just outside the snowline (r = 4.7 pc), they should not be blanets because they are more massive than the typical brown dwarf mass (∼3 × 104 ME ). Note that AGNs are often heavily obscured with dense gas even for hard X-rays (Buchner et al. 2014) (NH > 1023 cm−2, i.e., Compton-thick). If this is the case, the snowline is located at the inner region (e.g., r ∼ 2 − 3 pc), and as a result, blanets with Mbl ∼ 10ME − 100ME around MBH = 107 M⊙ could be possible. Our results suggest that blanets could be formed around relatively low-luminosity AGNs during their lifetime (≲108 yr). The system of blanets should be extraordinarily different from the standard Earth-type planets in the exoplanet systems. The blanets may acquire a rarefied atmosphere due to accretion of the gas in the circumnuclear disk (Section 4.3). The dynamical evolution of the swarm of blanets around an SMBH and whether they become more massive objects or are destroyed due to collisions may be an interesting subject for future studies (Section 4.2).
We would like to appreciate the anonymous referee's many valuable comments. The authors also thank Hidekazu Tanaka for many thoughtful comments. This work was supported by JSPS KAKENHI grant No. 18K18774.
Footnotes
- 5
Here, we merely call massive rocky/icy objects orbiting around a central gravity source as "planets."
- 6
This does not necessarily mean a simple abbreviation of "black hole planet," because this new class of objects does not resemble the planets in the solar system nor any known exoplanet systems, in a sense that a swarm of super-Earth mass objects are orbiting around the central gravity source. See also Section 4.2.
- 7
- 8
Here, we suppose water ice (Sato et al. 2016). In fact, the presence of H2O in AGNs is suggested by maser observations (e.g., Greenhill et al. 2003), and by chemical models (e.g., Wada et al. 2016). Note that vcrit is much smaller (∼1 m s−1) for silicate monomers (Wada et al. 2009). Therefore, we here consider dust evolution outside the snowline.
- 9
- 10
The effect of the collisional compression is negligibly small in this case.










